DSA，Data Structure and Algorithm
这两年完全没有精进，leetcode 也不会做。
保研面试前极限溜一遍两年前的 PPT…

基本概念

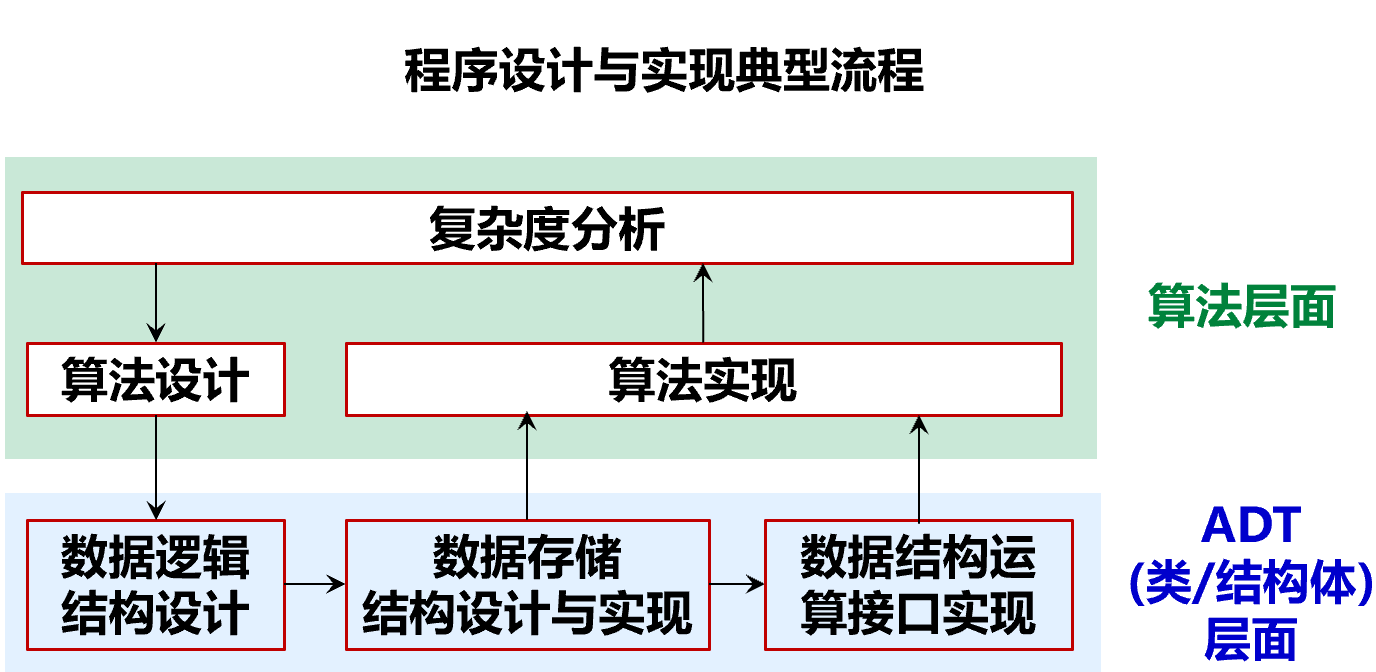
Overview of Data Structure

数据结构 = 逻辑结构 + 存储结构 + 数据操作

  • 逻辑结构 ：数据元素之间的关系（集合、线性表、树、图）
  • 存储结构 / 物理结构 ：数据在计算机中的存储方式。同一逻辑结构可以有多种存储结构。
    • 顺序存储 ：在内存中连续存储，所有元素的逻辑顺序与其物理存放顺序一致，支持随机访问
    • 链式存储 ：需要对所有元素的存储进行索引（头尾指针、索引表等）/ 哈希（存储关键码，通过散列函数计算存储位置）
  • 数据操作 ：建立，清除，求长，判空，判满，查找，获取，更新，插入，删除，遍历

抽象数据类型 (ADT) = 三元组 $(Data, Relation, Operation)$

  • ADT 就是 Struct 或 Class 本身
  • 数据结构就是 ADT 的设计与实现
  • 内置数据类型：int, float, char, bool，string 等
  • 标准库 std 实现的复合数据类型：vector, list, map, set, stack, queue 等

复杂度

符号 名称 含义
$O(f(n))$ 大O（上界） 最坏情况下，运行时间不会比某个常数倍的 $f(n)$ 大
$\Omega(f(n))$ 大Ω（下界） 最好情况下，运行时间至少是某个常数倍的 $f(n)$
$\Theta(f(n))$ 大Θ（紧确界） 最坏和最好情况的增长量级都等于 $f(n)$ （当这一点成立时才存在）

渐进复杂度 $O(·)$ 最常用。只考虑最高阶

递归

  • 两种思路：分治（二分查找）与减治（阶乘）
  • 复杂度用递推公式计算
  • 递归与迭代：递归的可读性好；但递归调用函数效率低；栈溢出风险。迭代写起来 dirty，但可能有更好的效率。

递归类似于脚本小子，迭代类似于自己造轮子

向量

线性表 + 顺序存储结构 + 动态内存分配（自动扩容）

秩（rank）：元素在线性表中的前驱数量，即元素的索引

1
2
3
4
5
6
7
8
9
template <typename T>
class vector {
private:
    T* data;          // 首地址
    int capacity;     // 容量
    int size;         // 当前元素个数
public:
    ... // 运算接口
};

运算接口

向量运算接口
向量运算描述
构造 构造函数
清除 析构函数
求长 size()
判空 isempty()
判满 isfull()
获取 get(r)operator[] 重载，随机访问
更新 put(r,e)
插入 insert(r,e)调用前会自动检查 size 与 capacity，必要时扩容。
扩容是将原有元素复制到新分配的更大内存中（通常是翻倍），然后销毁原有内存。
删除 remove(r)删除秩为 r 的元素，返回该元素中原存放的对象
查找 find(e)查找等于 e 且秩最大的元素，返回其秩；若查找失败则返回 -1。
cpp 的 std::vector 自带的是线查而不是二分
遍历 traverse遍历向量中所有元素，处理方法由函数对象指定
判序 disordered()判断所有元素是否已按降序排序
排序 sort()调整各元素的位置，使之按降序排序
去重 deduplicate()
有序向量的额外运算描述
去重 unify()双指针法，线性复杂度 $O(n)$
查找 search(e)多次查找的时候，对向量排序 + 二分的复杂度是 $O(nlogn + mlogn)$ ，而线查是 $O(mn)$

向量排序

  • 每次将一个元素插入到已排序的部分中（插入过程可用二分查找优化）
  • 稳定排序，$T = O(n^2)$，最好 $O(n)$（已有序）
插入排序 
1
2
3
4
5
6
7
8
9
10
11
12
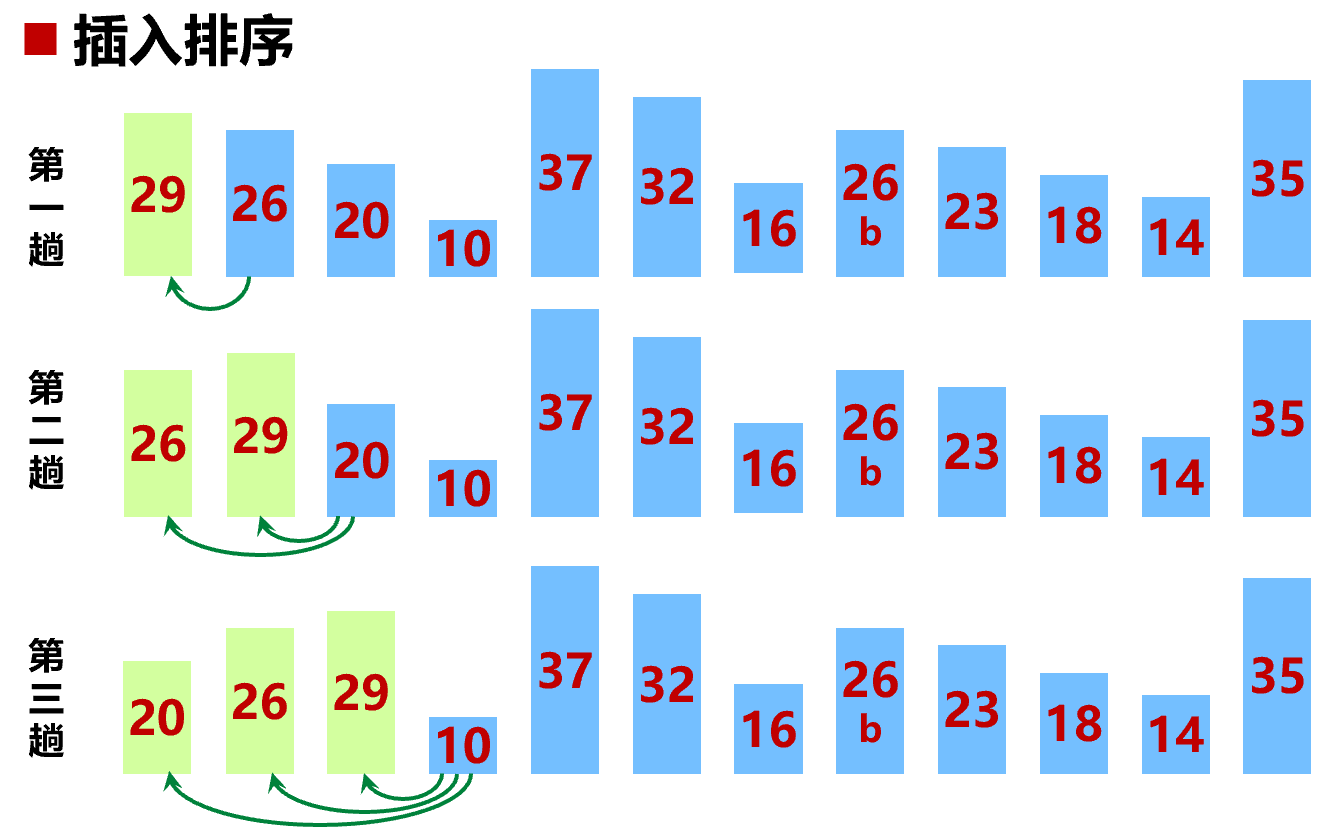
void insertion_sort(vector<int>& v) {
    int n = v.size();
    for (int i = 1; i < n; i++) {
        int key = v[i];
        int j = i - 1;
        while (j >= 0 && v[j] > key) {
            v[j + 1] = v[j];
            j--;
        }
        v[j + 1] = key;
    }
}
  • 相邻元素交换，每次冒泡出一个最大值（最小值）
  • 稳定排序，$T = O(n^2)$，优化后最好 $O(n)$（一轮未交换则说明已有序，中止）
冒泡排序 
1
2
3
4
5
6
7
8
9
10
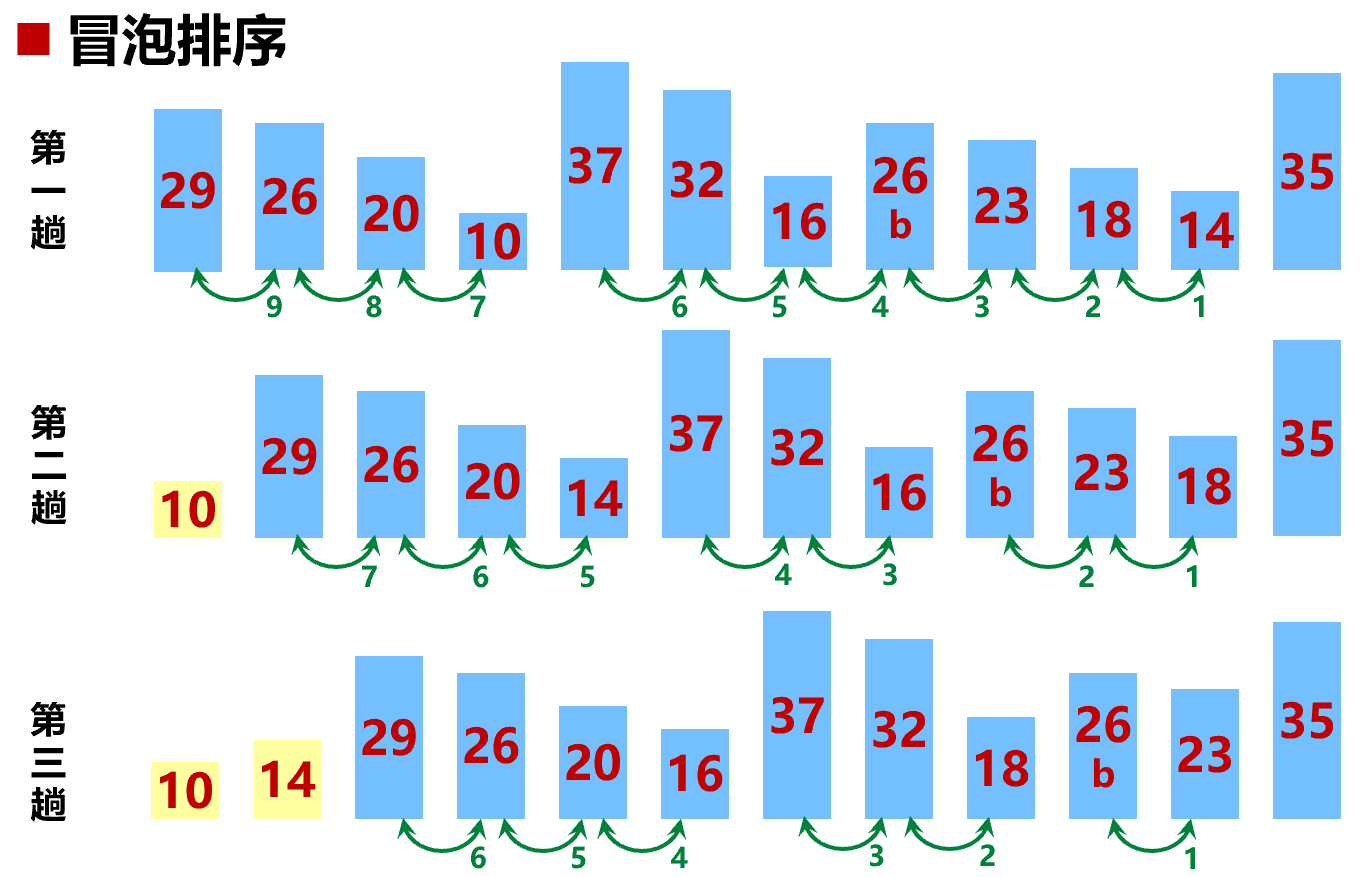
void bubble_sort(vector<int>& v) {
    int n = v.size();
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; ++j) {
            if (v[j] > v[j + 1]) {
                swap(v[j], v[j + 1]);
            }
        }
    }
}
  • 遍历未排序部分的最小值，与未排序部分的首元素交换（更新指针即可，只需最后进行一次 swap，无需过程中多次）
  • 不稳定排序，$T = O(n^2)$，过程中不涉及剩余元素内部的顺序调整，因此无法优化到 $O(n)$（遍历只是找到最值信息，完全忽略了其他信息），最好、最坏均为 $O(n^2)$
选择排序 
1
2
3
4
5
6
7
8
9
10
11
12
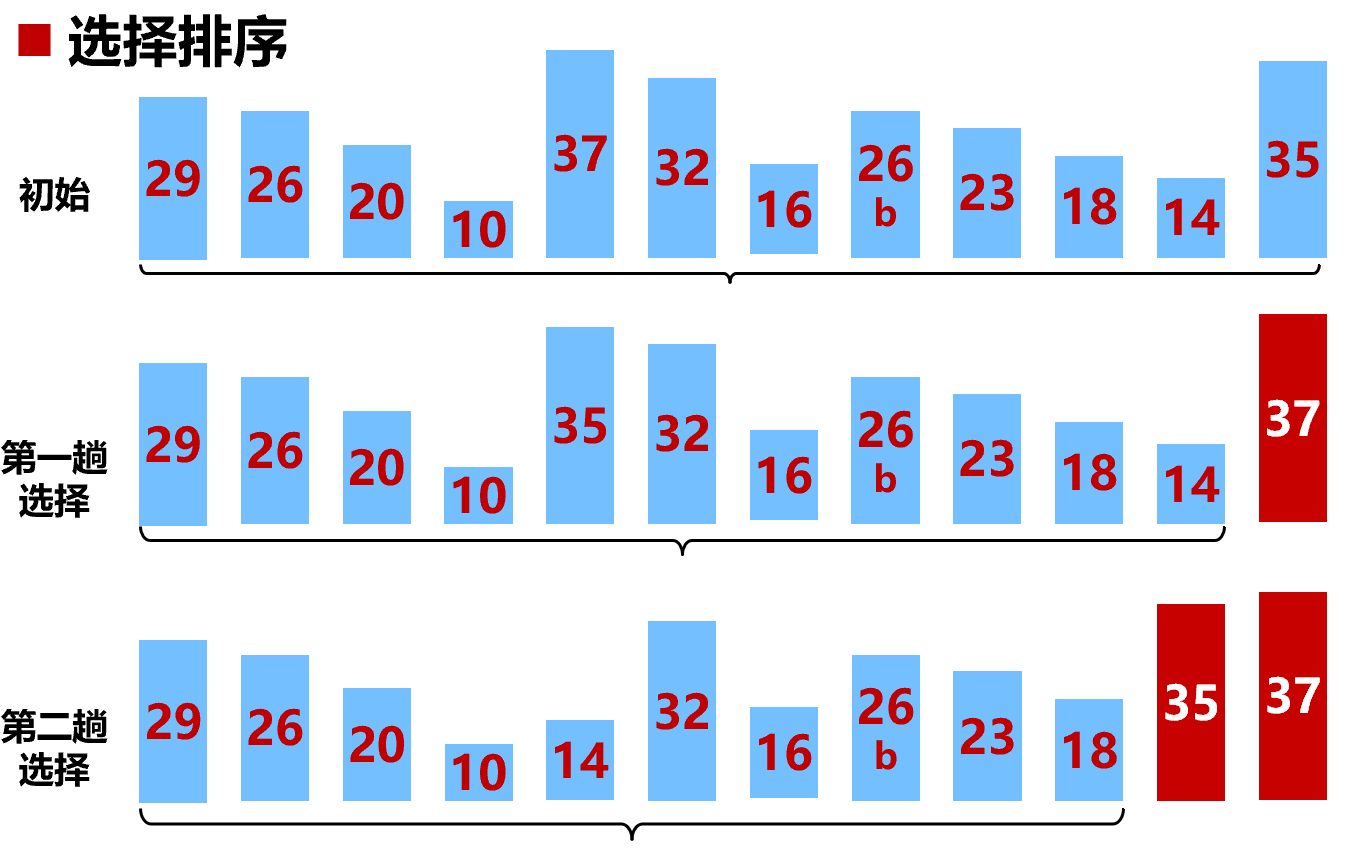
void selection_sort(vector<int>& v) {
    int n = v.size();
    for (int i = 0; i < n - 1; i++) {
        int min_index = i;
        for (int j = i + 1; j < n; ++j) {
            if (v[j] < v[min_index]) {
                min_index = j;
            }
        }
        swap(v[i], v[min_index]);
    }
}
  • 分治：先将向量分成两半返回有序子数组，然后合并两部分（双指针即可）
  • $T(n) = 2T(n/2) + O(n) \rightarrow T(n) = O(n \log n)$
  • 稳定排序，$T = O(n \log n)$，最好、最坏均为 $O(n \log n)$
  • 空间复杂度：每次合并需要额外开一个大数组存储合并结果，因此辅助空间复杂度为 $O(n)$
归并排序 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
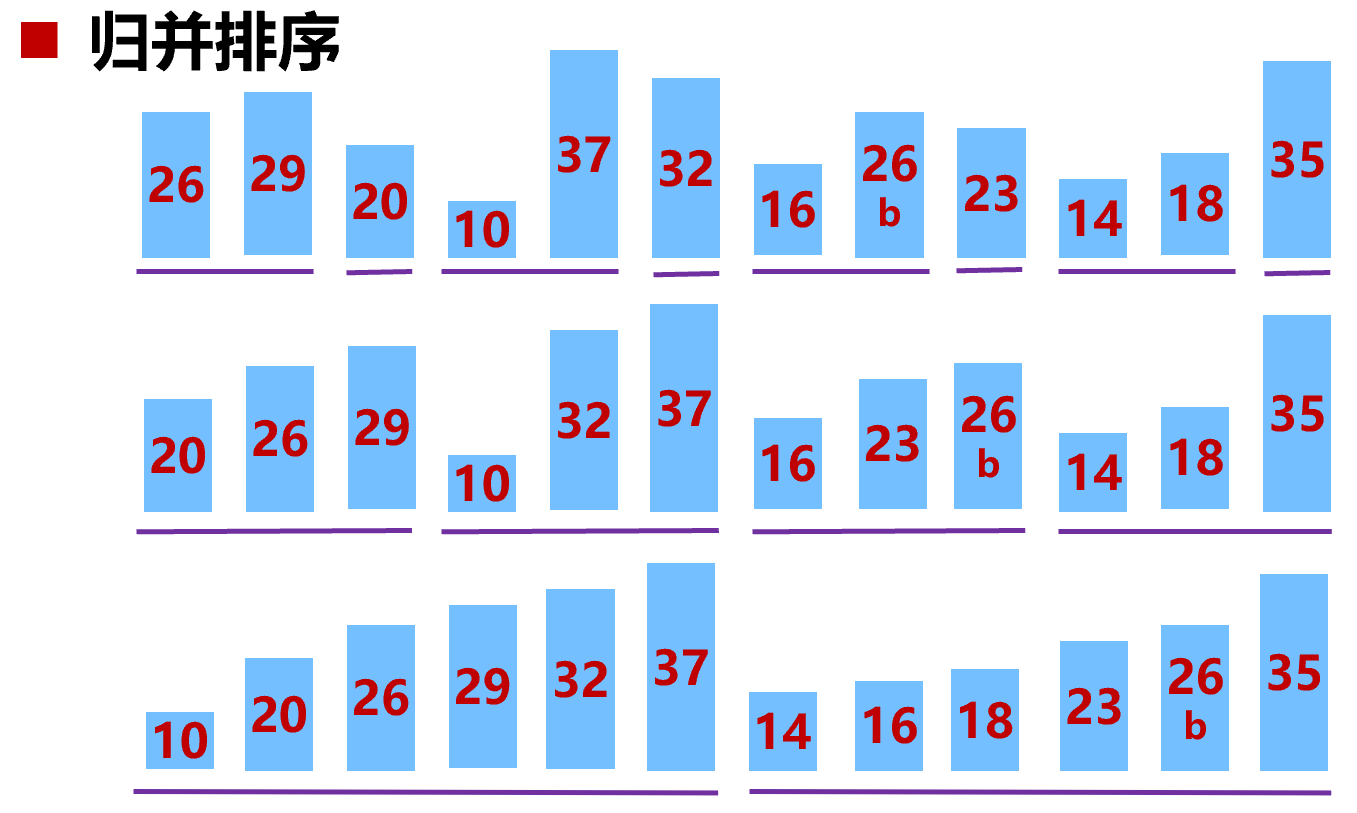
void merge(vector<int>& v, int left, int mid, int right) {
    int n1 = mid - left + 1;
    int n2 = right - mid;

    vector<int> L(n1), R(n2);
    for (int i = 0; i < n1; i++) L[i] = v[left + i];
    for (int j = 0; j < n2; j++) R[j] = v[mid + 1 + j];

    int i = 0, j = 0, k = left;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            v[k++] = L[i++];
        } else {
            v[k++] = R[j++];
        }
    }
    while (i < n1) v[k++] = L[i++];
    while (j < n2) v[k++] = R[j++];
}
void merge_sort(vector<int>& v, int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;
        merge_sort(v, left, mid);
        merge_sort(v, mid + 1, right);
        merge(v, left, mid, right);
    }
}
排序方法 最好时间 平均时间 最坏时间 辅助空间 稳定性
插入 $O(n)$ $O(n^2)$ $O(n^2)$ $O(1)$ 稳定
冒泡 $O(n)$ $O(n^2)$ $O(n^2)$ $O(1)$ 稳定
选择 $O(n^2)$ $O(n^2)$ $O(n^2)$ $O(1)$ 不稳定
归并 $O(n\log n)$ $O(n\log n)$ $O(n\log n)$ $O(n)$ 稳定

有序向量二分查找

直接在中点处返回没法得到秩最大的元素，接着向右搜即可

比较次数

二分查找流程图 & 比较次数

平均查找长度

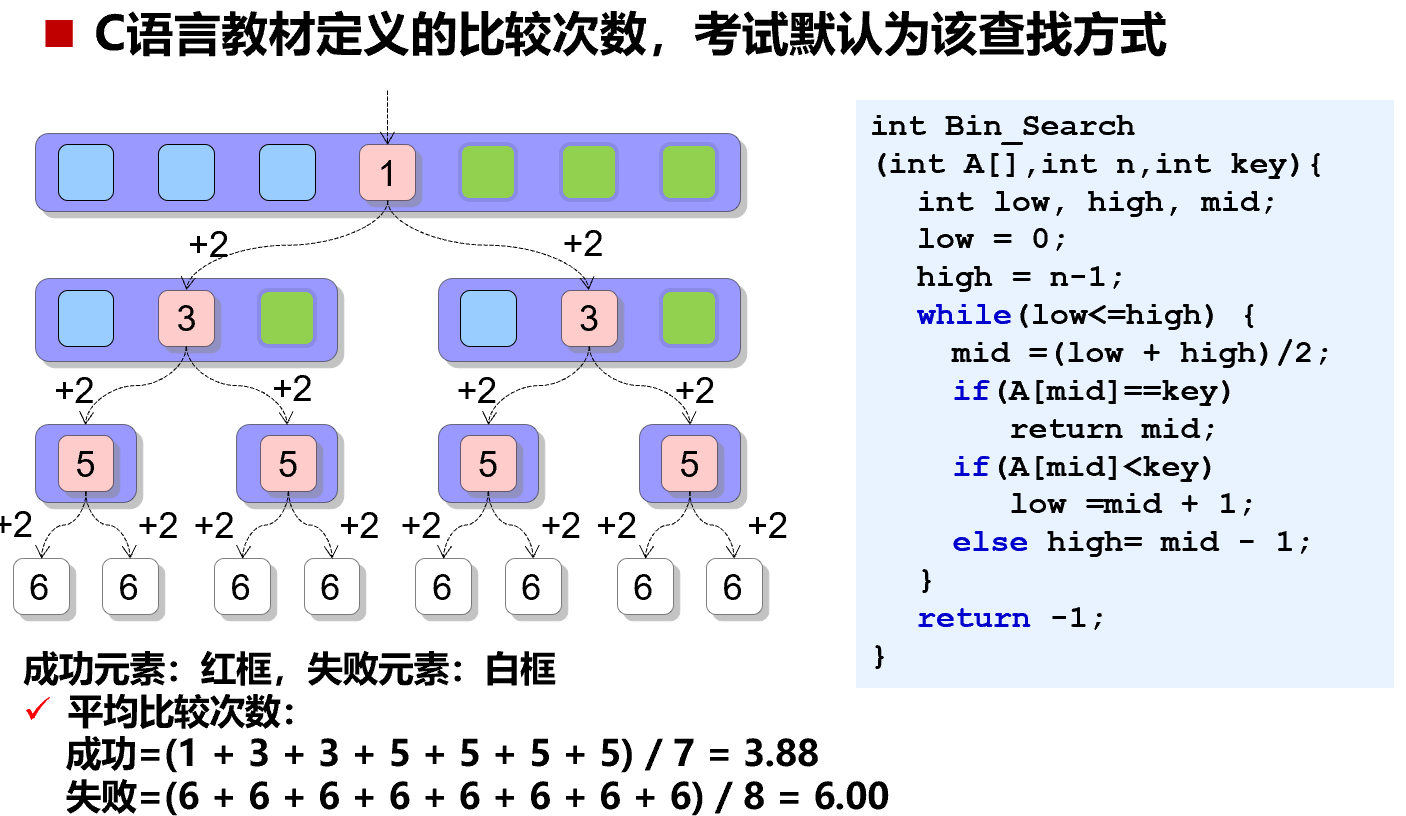
二分查找平均查找长度

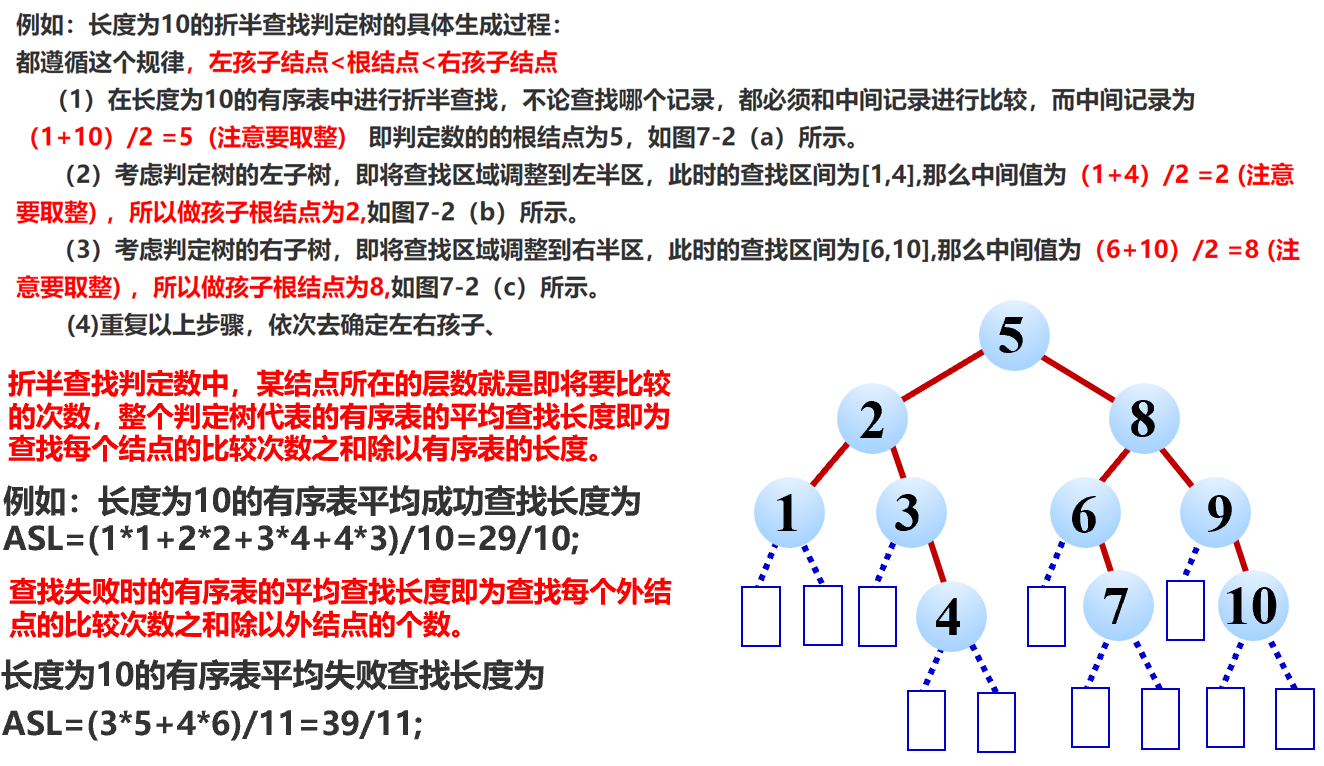
顺序查找 vs 二分查找

复杂度 无序查找 有序查找
单次 $O(n)$ $O(n \log n) + O(\log n)$
多次 $O(mn)$ $O(n \log n) + O(m \log n)$

列表

向量 和 列表 分别是 线性表 这一 逻辑结构 在 顺序存储 和 链式存储 这两种 存储结构 下的实现。std::vector 和 std::list 分别对应于 向量 和 列表。
列表 在这里指的是 链表 这种链式存储结构的线性表，在 cpp 标准库中对应于 std::list，而不是 python 里的 list（python 里的 list 实际上是动态数组，即向量）。

链式存储 ：内存无需连续分配，元素之间通过指针连接。

  • 只能局部访问，不能全局随机访问（向量的随机访问是通过索引直接计算全局地址）
  • 无需分配不需要的内存，没有空间浪费
1
2
3
4
struct Node {
    int data;          // 数据域，若干字节
    Node* next;       // 指针域，4 字节存储下一个节点的**地址**
};
1
2
3
4
class List {
private:
    Node* head;       // 头指针，指向链表的第一个节点
};
1
2
3
4
5
6
7
8
class List {
private:
    Node* head;       // 头指针，指向链表的第一个节点
    List(){
        head = new Node(); // 创建一个头结点
        head->next = nullptr; // 头结点的 next 之后再指向列表的第一个节点
    }
};

这里有没有表头节点到底啥区别？
注意，头节点的 data 是没有意义的，这是说 从 head->next 开始才是真正的数据项 ，表头结点的目的就是让新的节点插入和删除操作在表头时和非表头时更统一一些，不需要区分是不是在头部操作，因为对首元素的插入和删除也是在头节点之后进行的，从而简化实现。

单向链表的头节点和双向链表的头尾节点统称 哨兵节点（Sentinel Node），它们的作用是简化边界条件的处理。

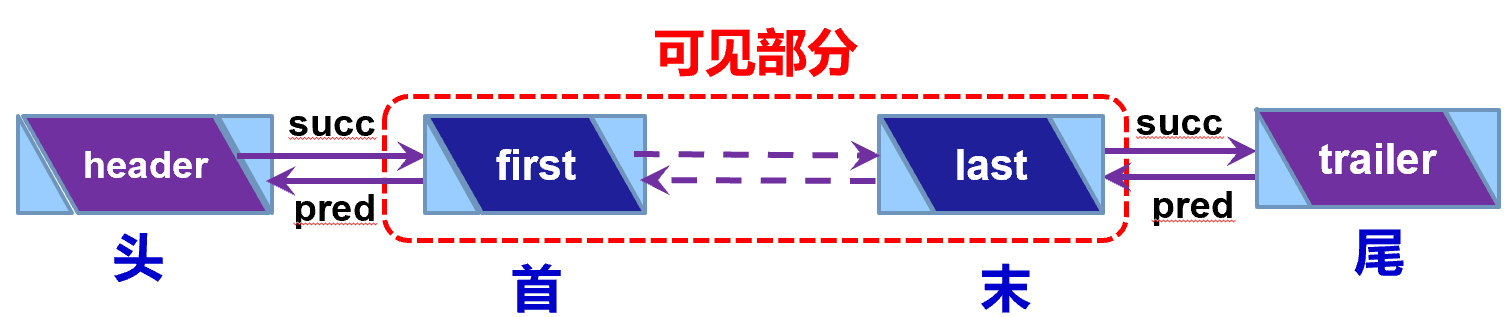
哨兵节点，对外部不可见，可见部分任意节点存在前驱和后继

以下都是针对 带表头 / 头尾结点 的单链表或双链表 ：

插入与删除

插入时要搞清楚插入前后拓扑关系，不能在这个过程中让某个节点的前驱或后继数为 0。

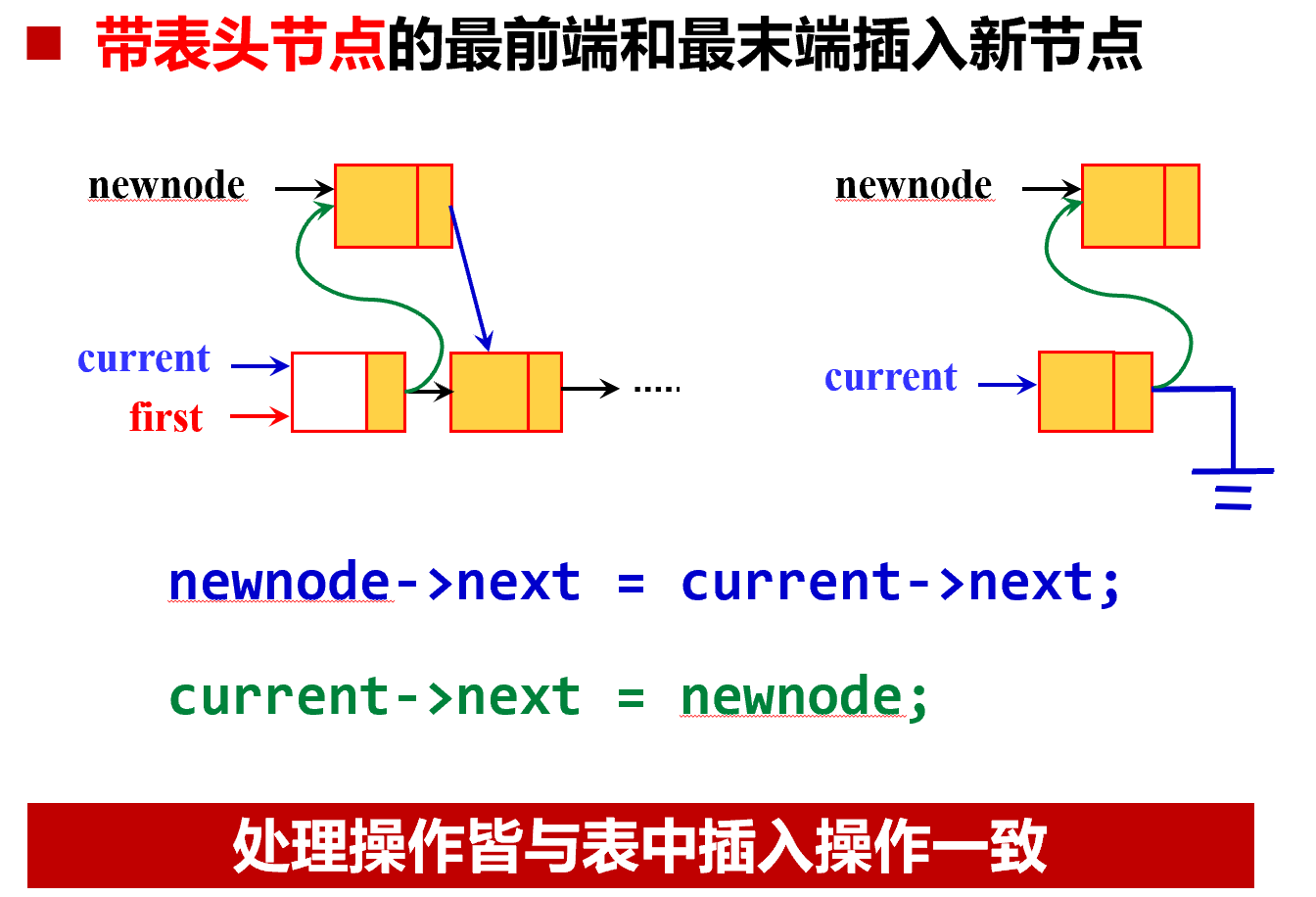
单链表插入

插入时要搞清楚插入前后拓扑关系，不能在这个过程中让某个节点的前驱或后继数为 0。双链表的插入需要连两个方向。

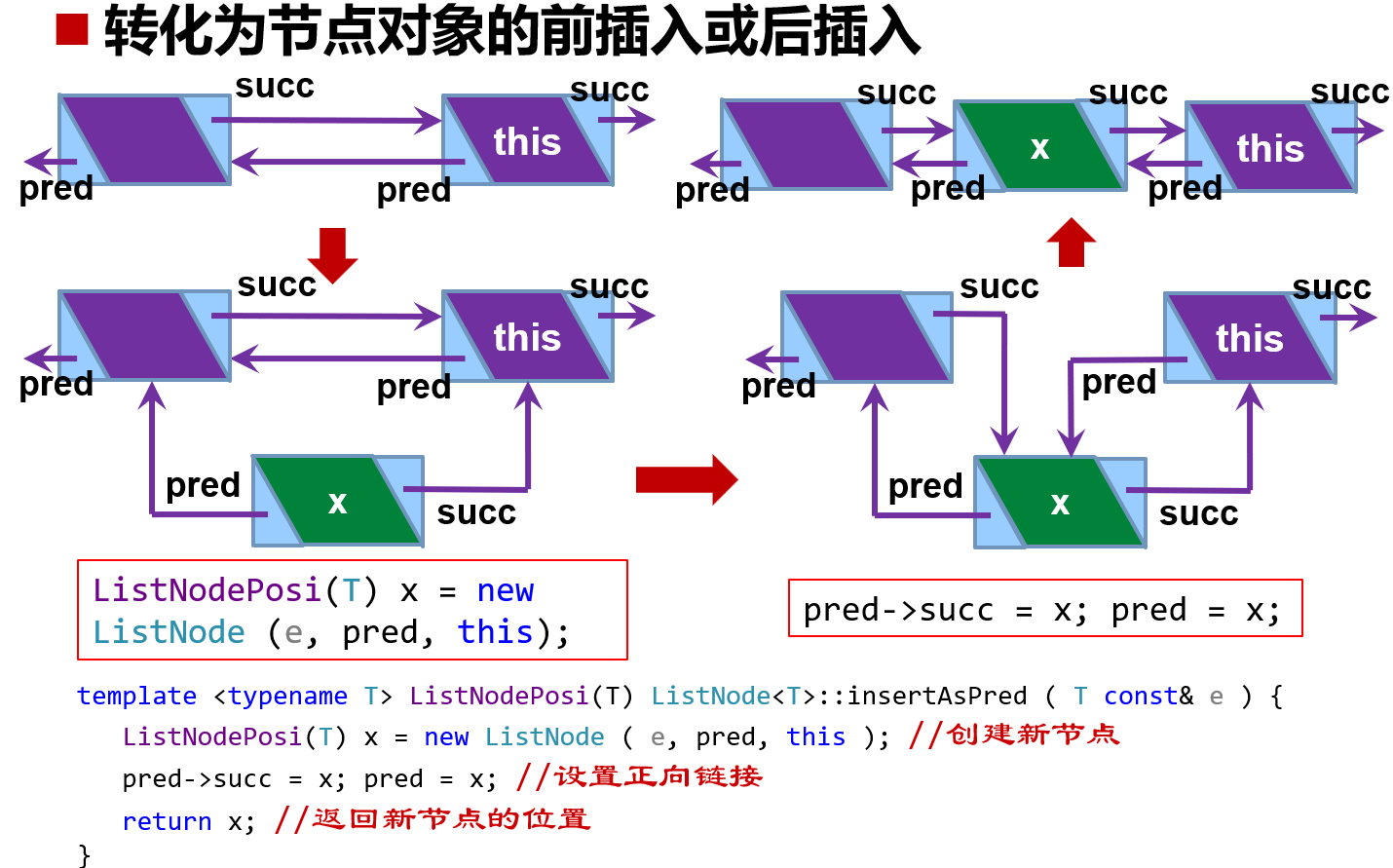
双链表插入

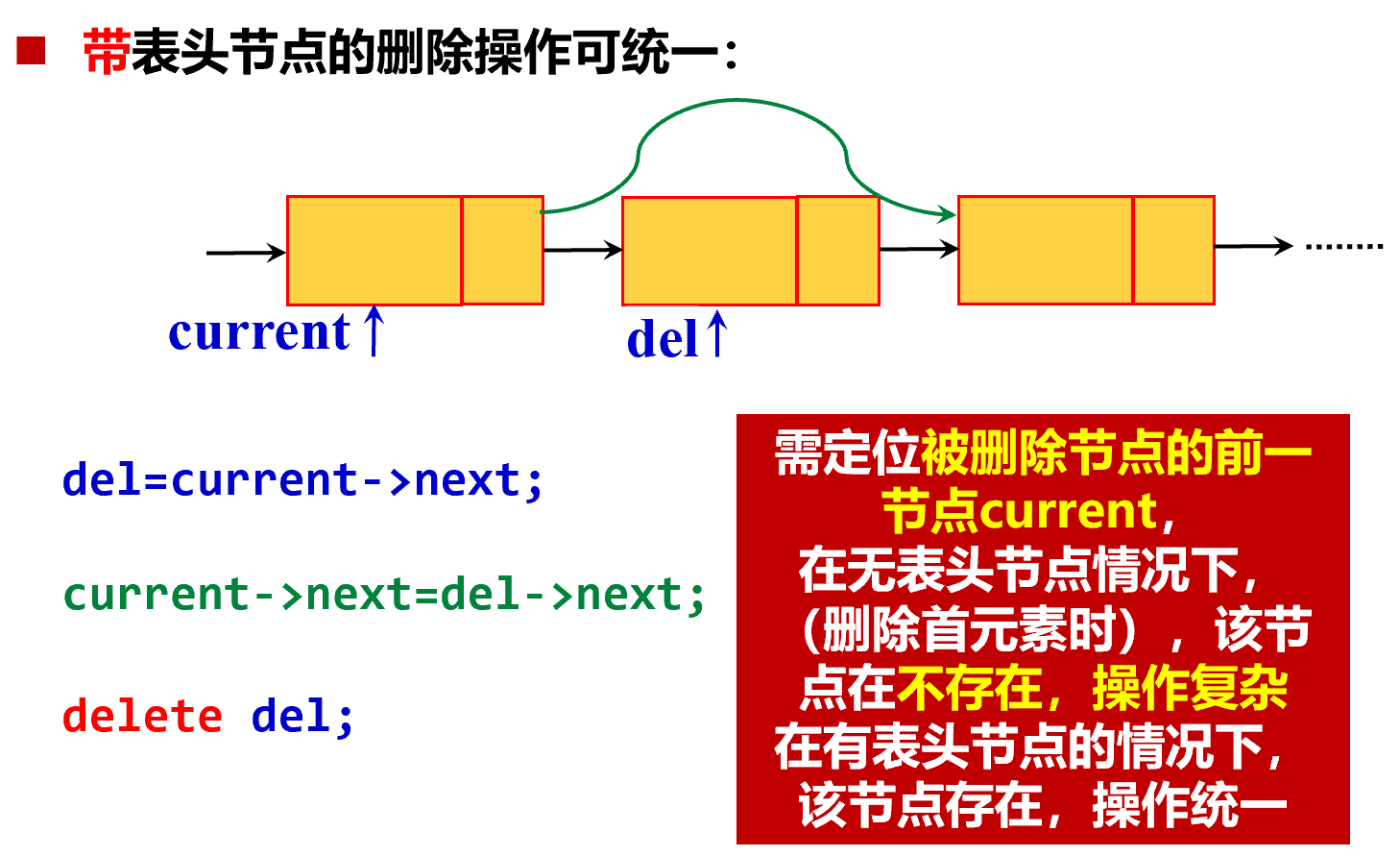
删除指定节点时，先找到前驱节点。另外重连以后要把原来的节点 delete 掉，释放内存，也就删了原来的边。

注意，单链表即使有额外的尾指针，删除尾节点时也需要从头遍历到倒数第二个节点，不能 $O(1)$ 删除。

单链表删除

前驱后继都得找。另外重连以后要把原来的节点 delete 掉，释放内存，删了两头的边。

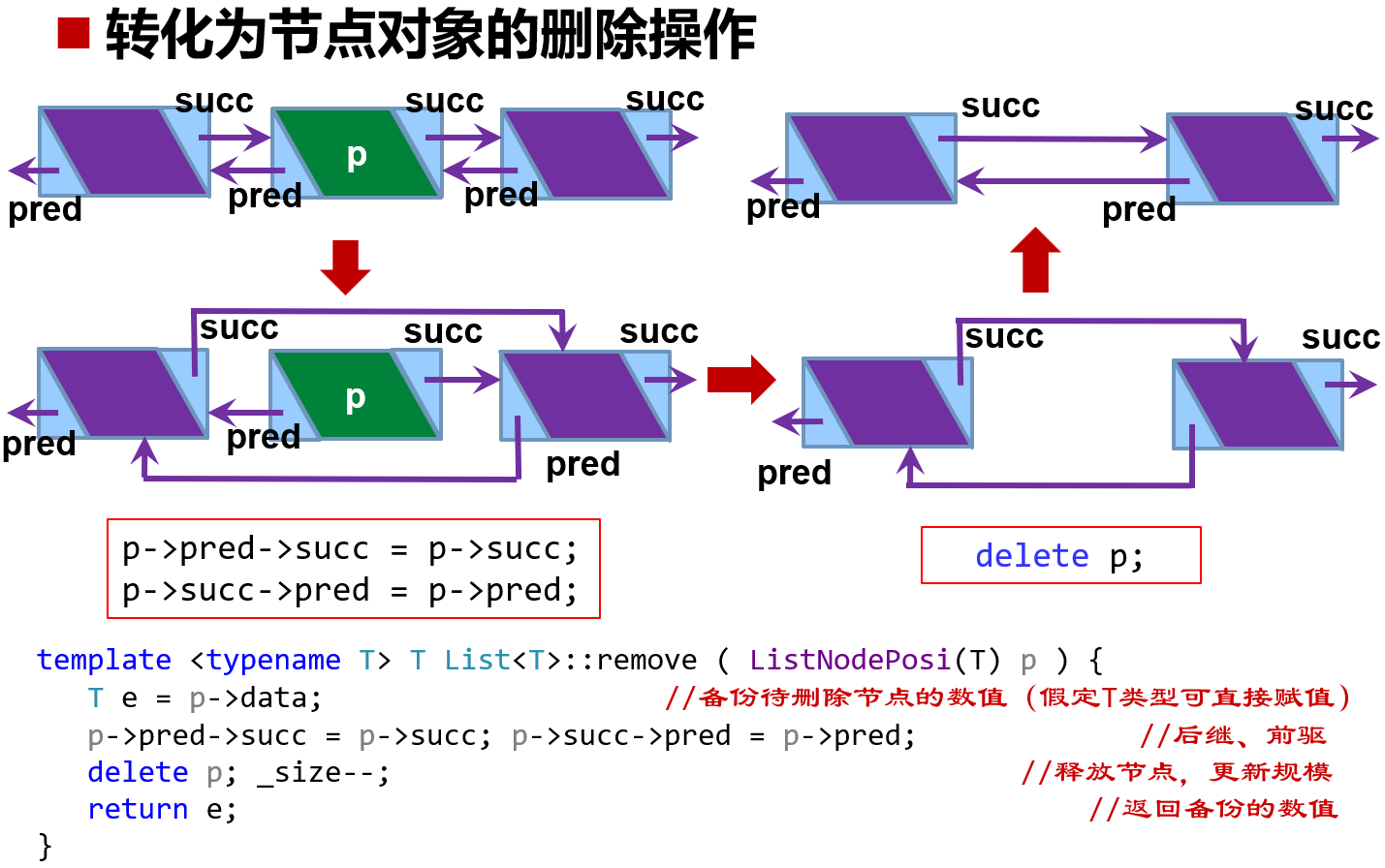
双链表删除

链表运算接口

析构函数 ：反复调用删除函数，把所有节点都删掉，再释放头尾节点。$O(n)$
有序链表的去重 ：双指针法，线性复杂度 $O(n)$
列表排序 ：

  • 列表的归并排序是就地排序，不占用额外空间；时间复杂度还是 $O(n \log n)$ （归并排序更适合用列表实现）
  • 列表的选择排序是稳定的，取决于其对多个最大值的处理方式
排序方法 最好时间 平均时间 最坏时间 辅助空间 稳定性
插入 $O(n)$ $O(n^2)$ $O(n^2)$ $O(1)$ 稳定
冒泡 $O(n)$ $O(n^2)$ $O(n^2)$ $O(1)$ 稳定
选择 $O(n^2)$ $O(n^2)$ $O(n^2)$ $O(1)$ 稳定
归并 $O(n\log n)$ $O(n\log n)$ $O(n\log n)$ $O(1)$ 稳定
排序方法 最好时间 平均时间 最坏时间 辅助空间 稳定性
插入 $O(n)$ $O(n^2)$ $O(n^2)$ $O(1)$ 稳定
冒泡 $O(n)$ $O(n^2)$ $O(n^2)$ $O(1)$ 稳定
选择 $O(n^2)$ $O(n^2)$ $O(n^2)$ $O(1)$ 不稳定
归并 $O(n\log n)$ $O(n\log n)$ $O(n\log n)$ $O(n)$ 稳定

向量 vs 列表

std::vector
std::list

栈

后进先出的线性表，可由向量或链表派生。

  • 向量实现：在 向量的末尾 插入和删除
  • 链表实现：在 链表的头部 插入和删除

接口 ： push(e) 入栈，pop() 出栈，top() 获取栈顶元素，isempty() 判空，size() 求长，均为 $O(1)$
应用 ：递归风格的问题。进制转换，括号匹配，表达式求值，函数调用栈，深度优先搜索等

括号匹配

扫描字符串，遇到左括号入栈，遇到右括号则 pop() 栈顶元素并判断是否匹配，最后对栈判空

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
bool is_balanced(const string& s) {
    stack<char> st;
    for (char c : s) {
        if (c == '(' || c == '{' || c == '[') {
            st.push(c);
        } 
        else if (c == ')' || c == '}' || c == ']') {
            if (st.empty()) return false; // 没有匹配的左括号
            char top = st.pop();
            if ((c == ')' && top != '(') ||
                (c == '}' && top != '{') ||
                (c == ']' && top != '[')) {
                return false; // 匹配失败
            }
        }
        else break; // 非括号字符，直接跳过
    }
    return st.empty(); // 栈空则匹配成功
}

表达式求值

表达式

中缀表达式 前缀表达式 后缀表达式
(x + y) * z * + x y z x y + z *
  • 中缀表达式 ：<操作数1> <操作符> <操作数2>，计算机难以解析
  • 前缀（波兰）表达式 ：<操作符> <操作数1> <操作数2>，操作符唯一对应于它后面的两个操作数
  • 后缀（逆波兰）表达式 ：<操作数1> <操作数2> <操作符>，操作符唯一对应于它前面的两个操作数

表达式求值包括 中缀转后缀 和 后缀求值 两个在扫描输入字符串时交替进行的过程，需要维护 操作符栈 和 操作数栈

后缀表达式求值

在扫描过程中将操作符放入操作符栈，随后再下次扫描到操作符时，进行操作符优先级判断

  • 若新操作符优先，栈顶元素无法弹出，新操作符入栈，扫描下一位
  • 若栈顶优先，则弹出栈顶，到操作数栈中取出操作数运算并将结果压入操作数栈，然后一直循环直到栈顶元素优先级不再更高（这时只能是相等），进入下一点的操作
  • 若优先级相等，只有 右括号碰到左括号 或 字符串结尾的哨兵字符 \0 碰到开始投入操作符栈底的哨兵字符 \0 这两种情况，继续扫描
    中缀转后缀

维护操作数栈这个过程比较复杂，但是原则可以归结为以下两点：

  1. 为了把操作数都压入栈后再执行运算。比如 A + B，在这个过程中，扫描的顺序是 A --> + --> B --> \0，这可以让 A 和 B 都入操作数栈后，扫描到 \0 时 + 再根据优先级判定而弹出操作符栈，并到操作数栈中取出 A 和 B 进行运算，这是为了调整中缀读取顺序与后缀运算顺序的方法；
  2. 整理操作符优先级关系。pri[][] 数组定义的优先级关系比较复杂，但核心思想就是，操作符总要出栈去做运算，优先级高的要先在后缀式中运算，因此需要先出栈。所以每次扫描新的操作符后，如果现在的操作符栈顶优先级更高，就可以出栈运算（可想而知，如果原来栈里没有括号，那这一步应该把栈里所有的都放出去；如果有括号，就放到最近的括号为止）；如果新扫描的操作符优先级更高，可能后面还有更高的，就先入栈等待后边出站的时机。

然后是 后缀表达式求值 的全过程，交替进行 操作数入栈，操作符入栈，操作符出栈，操作数与操作符运算，结果入栈 的过程，得到 后缀表达式 与 计算结果。

代码实现
后缀表达式求值

栈混洗与卡特兰数

对长度为 $n$ 的栈进行混洗，得到的序列数目为 卡特兰数

$$h(n) = \sum_{i=0}^{n-1} h(i) \cdot h(n-1-i)$$

$$h(n) = C_{2n}^{n} - C_{2n}^{n+1} = \frac{1}{n+1} C_{2n}^{n}$$

h(0) = 1，h(1) = 1，h(2) = 2，h(3) = 5，h(4) = 14，h(5) = 42，h(6) = 132，h(7) = 429

一些经典的问题

  • 括号匹配，借书还书，买票找零，栈混洗
  • 二叉树的不同结构数，上三角路径数，凸 $n+2$ 边形的三角剖分数

解决思路基本上是 $\sum_{i=0}^{n-1} h(i) \cdot h(n-1-i)$，即将问题分解为 「根节点」 + 两个独立子问题的和。

可行栈混洗序列的判断
一边顺序入栈一边与目标序列比较，如果入栈次数已经为序列长度（此后一定全是出栈），下一次与对应目标元素还不匹配，就说明不可能了。

可行栈混洗序列的判断

队列

先进先出的线性表，同时维护队头 front 和队尾 rear 指针。

对于单链表实现，表头为队头（方便删除），表尾为队尾（方便插入）。对于向量实现，队头为向量的首元素，队尾为向量的末元素。

接口 ：enqueue(e) 入队，dequeue() 出队，front() 获取队头元素，isempty() 判空，size() 求长，均为 $O(1)$

数组实现的 dequeue() 不需要移动所有元素，而是把 front 指针向后移动一位。

循环队列 ，元素个数为 (rear - front + n) % n，其中 n 是队列容量，front 指向队头前一位置，rear 指向队尾位置。

循环队列提高内存利用率，但仍无法解决内存满溢问题
注意 front 是相对地址或下标小的那个，在 rear 前面，循环队列中的元素是从 front --> rear 这一段空间所覆盖的